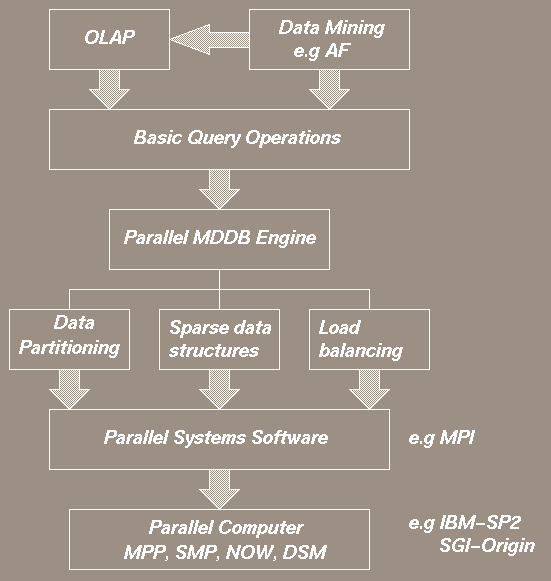
The multi-dimensionality of the underlying problem can be represented both in relational and multi-dimensional databases, the latter being a better fit when query performance is the criteria for judgment. Relational databases are scalable in size for OLAP and multidimensional analysis and efforts are on to make their performance acceptable. On the other hand multi-dimensional databases have proven to provide good performance for such queries, although they are not very scalable. In this project we are addressing scalability in multi-dimensional systems for OLAP and multi-dimensional analysis.
Multidimensional databases store data in multidimensional structure on which analytical operations are performed. A challenge for these systems is how to handle large and sparse data sets with large dimensionality. Parallel computing is necessary to address the performance issues for these data sets.
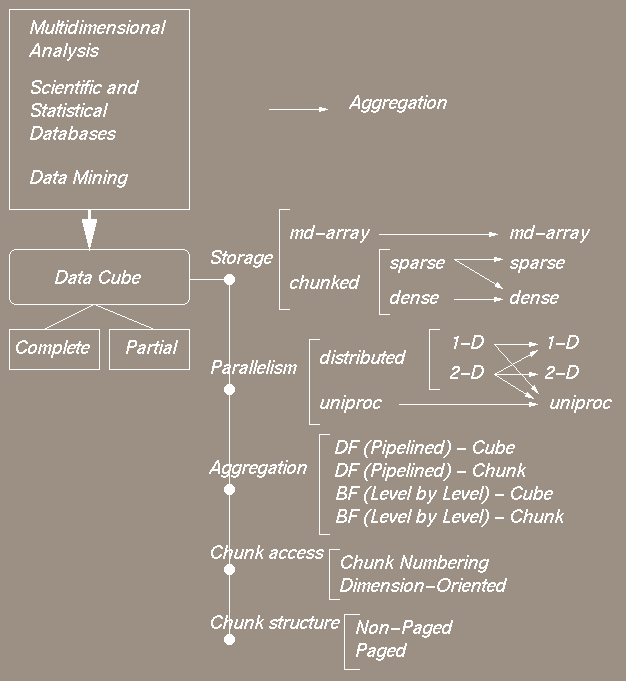
Chunking is used to store data either as a dense block using
multi-dimensional arrays or
a sparse set using a Bit encoded sparse structure (BESS). Chunks provide a
multi-dimensional index structure for efficient dimension oriented data
accesses much the same as multi-dimensional arrays do. Operations
within chunks and between chunks are a combination of relational and
multi-dimensional operations depending on whether the chunk is sparse or
dense.
In this research we address issues of data partitioning, parallelism, schedule construction, data cube building, chunk storage and memory usage on a distribute memory machine architecture. The following figures summarize the various available options, especially in terms of storage of cubes, parallelism at different levels, aggregation calculation orderings and the chunk access for aggregations.


Discovery of quantitative rules is associated with quantitative
information from the database. The data cube represents quantitative
summary information for a subset of the attributes. Transaction data
can be used to mine association rules by associating and
for each rule. Support of a pattern A in a set S
is the ratio of the number of transactions containing A and the
total number of transactions in S. Confidence of a rule A
-> B is the probability that pattern B occurs in S when
pattern A occurs in S and can be defined as the ratio of the
support of AB and support of A. The rule is then described as A
-> B [support, confidence] and a association
rule has a support greater than a pre-determined minimum support and a
confidence greater than a pre-determined minimum confidence. This can
also be taken as the measure of ``interestingness'' of the
rule. Calculation of support and confidence for the rule A
-> B involve the aggregates from the cube AB, A and
ALL. Additionally, dimension hierarchies can be utilized to provide
multiple level data mining by progressive generalization (roll-up) and
deepening (drill-down). This is useful for data mining at multiple
concept levels and interesting information can potentially be obtained
at different levels.
In this research we integrate data mining tasks with OLAP functionalities and
perform the following data mining tasks in parallel in our framework.
Association rule mining has applications in cross-marketing, attached mailing,
add-on sales, store layout and customer segmentation based on buying
patterns to name a few.
Some applications of classification are in similar patterns detection
for finding fraud, marketing to those potential customers who match
the pattern of previous successful sales, healthcare treatments that
are deemed cost-effective when they fit the pattern of success in
previous patients, and investment decisions are made on patterns of
previous gain are some application areas among many others.
Some applications of clustering are in creation of thematic maps in
geographic information systems by clustering feature spaces, detection
of clusters in satellite image data, Clustering of Web-log database to
discover groups of similar access patterns which may correspond to
different user profiles, or buying behavior in E-commerce systems,
Identification of clusters of data on disks and tapes for efficient storage
and retrieval of large scale scientific experimental data.
We present MAFIA (Merging Adaptive Finite IntervAls), which 1)
proposes adaptive grids for fast subspace clustering and 2) introduces
a scalable parallel framework on a shared-nothing architecture to
handle massive data sets. Performance results on very large data sets
and a large number of dimensions show very good results, making an
order of magnitude improvement in the computation time over current
methods and providing much better quality of clustering. Association Rules
Scalable and parallel association rule mining with attribute-oriented and attribute focusing methods for large data sets
Classification
Scalable and parallel decision tree based classification algorithms
Clustering
Scalable and parallel density and grid based clustering algorithms for large data sets in large number of dimensions, also incorporating subspace clustering
Clustering
Project Members: Sanjay Goil, Harsha Nagesh and Alok Choudhary
MAFIA : Efficient and Scalable Subspace Clustering for Very Large Data Sets
Clustering techniques are used in database mining for finding
interesting patterns in high dimensional data. These are useful in
various applications of knowledge discovery in databases. Some
challenges in clustering for large data sets in terms of scalability,
data distribution, understanding end-results, and sensitivity to input
order, have received attention in the recent past. Recent approaches
attempt to find clusters embedded in subspaces of high dimensional
data. In this research we propose the use of adaptive grids for efficient
and scalable computation of clusters in subspaces for large data sets
and large number of dimensions. The bottom-up algorithm for subspace
clustering computes the dense units in all dimensions and combines
these to generate the dense units in higher dimensions. Computation is
heavily dependent on the choice of the partitioning parameter chosen
to partition each dimension into intervals (bins) to be tested for
density. The number of bins determines the computation requirements
and the quality of the clustering results. Hence, it is important to
determine the appropriate size and number of the bins.